22. Parametric Surfaces and Surface Integrals
c. Scalar Surface Integrals
2. Formulas
On the previous page, we defined the scalar differential of surface area to be \[ dS=|\vec{N}|\,du\,dv \] which gives the area of an infinitesimal coordinate grid rectangle. Now that we know \(dS\), integrating a scalar on a parametric surface is straightforward. The most difficult part is finding the limits on the integral.
The integral of a scalar \(f(x,y,z)\) over a surface, \(S\), parametrized as \(\vec R(u,v)\) is \[ \iint_S f\,dS =\iint_{\vec R} f(\vec R(u,v))|\vec{N}|\,du\,dv \] Note that the function must be evaluated on the surface and the \(u\) and \(v\) limits must be put on the integrals.
The simplest example is the area of a surface, \(S\), which is \[ A=\iint_S 1\,dS =\iint_S |\vec{N}|\,du\,dv \] This and other applications (mass, center of mass, centroid and average value) appear on subsequent pages.
Find the area of the piece of the cylinder \(x^2+z^2=4\) between \(y=0\) and \(y=10+2x+3z\) parametrized by \(\vec R(\theta,y)=\left\langle 2\cos\theta,y,2\sin\theta\right\rangle\). The ranges and normal were found in previous exercises.
We previously found the length of the normal is \(|\vec{N}|=2\) and the ranges are \(0 \le \theta \le 2\pi\) and \(0 \le y \le 10+4\cos\theta+6\sin\theta\). We need to put the \(y\) integral inside of the \(\theta\) integral because the \(y\) range is a function of \(\theta\). So the area is \[\begin{aligned} A&=\iint_S 1\,dS =\iint_S |\vec{N}|\,dy\,d\theta =\int_0^{2\pi}\int_0^{10+4\cos\theta+6\sin\theta} 2\,dy\,d\theta \\ &=\int_0^{2\pi} \left[2y\dfrac{}{}\right]_{y=0}^{10+4\cos\theta+6\sin\theta}\,d\theta =\int_0^{2\pi} 2(10+4\cos\theta+6\sin\theta)\,d\theta \\ &=2\left[10\theta+4\sin\theta-6\cos\theta\dfrac{}{}\right]_0^{2\pi} =2(10\cdot2\pi)=40\pi \end{aligned}\]
Compute \(\displaystyle \iint_S \dfrac{1}{\sqrt{4x^2+4y^2+25}}\,dS\) over the piece of the paraboloid \(z=\dfrac{x^2+y^2}{5}\) below \(z=5\). The tangent vectors were found in a previous exercise.
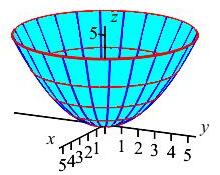
The normal is the cross product of the tangent vectors. Further, \(dS=|\vec N|\,dr\,d\theta\). There is no extra \(r\).
\(\displaystyle \iint_S \dfrac{1}{\sqrt{4x^2+4y^2+25}}\,dS=\dfrac{4\pi}{5}\)
From the previous exercise, the parametrization and tangent vectors are: \[\begin{aligned} \vec R(r,\theta)&=\left\langle r\cos\theta,r\sin\theta,\dfrac{r^2}{5}\right\rangle \\ \vec e_r&=\left\langle \ \cos\theta,\quad\sin\theta,\;\dfrac{2r}{5}\right\rangle \\ \vec e_\theta&=\left\langle -r\sin\theta,r\cos\theta,\;0\right\rangle \end{aligned}\] Then the normal vector and its length are: \[\begin{aligned} \vec N&=\left\langle -\,\dfrac{2r^2}{5}\cos\theta, -\,\dfrac{2r^2}{5}\sin\theta,r\right\rangle \\ |\vec N|&=\sqrt{\dfrac{4r^4}{25}\cos^2\theta +\dfrac{4r^4}{25}\sin^2\theta+r^2}=r\sqrt{\dfrac{4r^2}{25}+1} \end{aligned}\] The integrand is: \[ \dfrac{1}{\sqrt{4x^2+4y^2+25}}=\dfrac{1}{\sqrt{4r^2+25}} \] So the integral is: \[ \iint_S \dfrac{1}{\sqrt{4x^2+4y^2+25}}\,dS =\int_0^{2\pi}\int_0^2 \dfrac{1}{\sqrt{4r^2+25}}|\vec N|\,dr\,d\theta \]
Notice that there is NO extra \(r\) in the integrand before the \(dr\,d\theta\)! This is because \(r\) and \(\theta\) are not actually polar or cylindrical coordinates. They are the parameters for a surface which just happen to have the same names. The \(|\vec N|\) plays the roll of the Jacobian.
We continue the computation of the integral: \[\begin{aligned} \iint_S \dfrac{1}{\sqrt{4x^2+4y^2+25}}\,dS &=\int_0^{2\pi}\int_0^2 \dfrac{1}{\sqrt{4r^2+25}} r\sqrt{\dfrac{4r^2}{25}+1}\,dr\,d\theta \\ &=2\pi\int_0^2 \dfrac{r}{5}\,dr =2\pi\left[\dfrac{r^2}{10}\right]_0^2=\dfrac{4\pi}{5} \\ \end{aligned}\]
We emphasize, if you are dealing with a parametric surface where the parameters are \(r\) and \(\theta\), there is NO extra \(r\) in the integrand before the \(dr\,d\theta\)! This is because \(r\) and \(\theta\) are not actually polar or cylindrical coordinates. They are the parameters for a surface which just happen to have the same names. The \(|\vec N|\) plays the roll of the Jacobian.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum